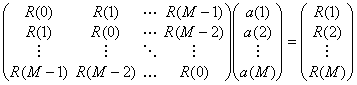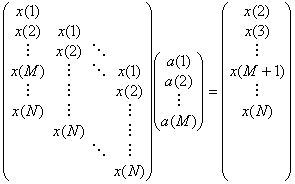ex1113.html（時系列解析／演習：ＡＲモデルの同定）

今日の例題「ＡＲモデルの同定」

解説：　ＡＲ（自己回帰）モデルによる時系列の予測　
時系列 x(s) のＡＲモデルによる予測は，以下の式で与えられる。

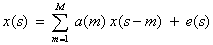
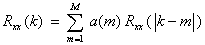
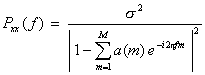
ここで，a(m) はＡＲ係数で，e(s) は予測誤差である。いま次数Ｍが最適な大きさで，この式が最良な線形予測（予測誤差の2乗平均が最小）になっているとすると，e(s) は x(s-k)，k=1,2,･･･とは全く相関のない白色雑音になってはずである。したがって，この式に x(s-k) をかけて期待値を取る操作を行うと，このときのＡＲ係数が満足すべき，以下のYule-Walker方程式が得られる。
時系列の自己共分散関数 E[x(s)x(s-k)] = Rxx(k) が与えられれば（適切に推定しておけば），この式から，ＡＲ係数を求めることができる。ＡＲ係数が定まれば，時系列 x(s) のパワースペクトルは，以下の式で与えられる。ここで，σ^2は予測誤差の分散である。
例題プログラム：　[ ar_model.m ]
次のプログラムでは，3つの正弦波に少し正規白色雑音を加えた時系列を例として，まず，その時系列に対してYule-Walker法によるＡＲモデルの推定を行っている。また，そのスペクトルを求めて，Welch法によるFFTスペクトルと比較している。さらに，そのＡＲモデルによる予測を行って，与えられた時系列と予測した時系列がどれほど良く一致するか比較している。
　オリジナルのプログラムは，こちらから，ダウンロード

% ar_model.m　 %　 % ＜　AR_model identification ＞　 %　 Fs = 200; T = 1; N = Fs*T;　 t = (0:1/Fs:T-1/Fs);　 rn = 0.02*randn(size(t));　 %　 % ----------------------signal---------------------------　 x = sin(2*pi*2*t) + sin(2*pi*10*t) + sin(2*pi*25*t) + rn;　 % -------------FFT spectrum (Welch's method)-------------　 [Pxx,f] = psd(x,256,Fs,hanning(256),128,'none'); 　 % -------------------------------------------------------　 %　 % AR model estimation 　 %　 M = 4;　　　　　　　　　　　　% order of AR model 　＜---かえてみよう [a,e] = aryule(x,M);　　　　　　　　　　% Yule-Walker method　 %　e: variance of prediction error % [a,e] = arburg(x,M);　　　　　　　　　% Burg method　 Pxx_ar = e*abs(freqz(1,a,N/2,Fs)).^2;　　% spectrum (AR model)　 f_ar = (0:1/T:Fs/2-1/T);　 %　 subplot(311);plot(f,10*log10(Pxx),'-b',f_ar,10*log10(Pxx_ar),':r');　 legend('Pxx (FFT spectrum)','Pxx (AR spectrum)')　 ylabel('Magnitude (dB)'); xlabel('Frequency (Hz)');　 %　 % prediction by the AR model　 %　 y = zeros(1,N);　 a(1) = [];　 for I=M+1:N　 for J=1:M　 y(I)=y(I)-a(J)*x(I-J);　 end　 end　 % ------------------------------　 xest = y(M+1:N);　 t(1:M) = [];　 x(1:M) = [];　 subplot(312);plot(t,x,'-b',t,xest,':r');ylabel('Amplitude')　 axis([0,T,-3,3]);legend('x (obserbed)','x (predicted)')　 subplot(313);plot(t,x-xest);　 axis([0,T,-0.5,0.5]);legend('x-xest')　 ylabel('Prediction Error'); xlabel('Time (sec)');　 % ------------------------------　
演習：　例題プログラムを実行してみよう
まず実行してみて，このプログラムの内容をよく理解してください。
さて，モデルの次数はどれぐらいが良いでしょうか？
- 予測誤差に周期性が認められるということは？
- モデル次数をかえてみてください。
- スペクトルが3つのピークを持つようにするためにはAR次数は最低いくつ必要でしょうか？
- 鋭いスペクトルをもつ時系列には，Burg法のほうが良い？

今週の課題

ＡＩＣによる最適なＡＲモデルの選定
最適なＡＲモデル，つまり最適な次数をどのように決定したらよいであろうか？
次数Ｍを大きくすれば，予測誤差の分散σ^2は，どんどん小さくなっていく。だからといって，Ｍは大きいほど良いと考えるのは正しくない。なぜなら，我々は，観測された時系列，つまりあるメカニズムから確率的に生起された1つの標本 x(s) に対してモデルのあてはめを行っているにすぎない。たまたまそのときのノイズの現れ方まで正確に表現できるようにと，無用に大きな次数にすると，そのメカニズムから生成された別の標本に対しては，かえって予測が悪くなってしまうのである。（つまり我々は得られた時系列を説明するモデルが必要なのではなく，その時系列を生成するメカニズムのモデルが欲しいのだ！）
　最適なモデル次数を選択する基準のひとつにＡＩＣ（Akaike's Information Criterion）がある。Ｍ次ＡＲモデルに対するＡＩＣは，次式で計算することができ，この値が小さいものほど良いモデルと見なせる。（ＡＩＣの理論的な詳細については，テキスト８章を各自勉強してください。）

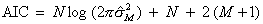
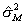ここで，Nはデータ点数，Mはモデル次数，は，予測誤差の分散（推定値）である。
　上の例題プログラムを，ＡＩＣを計算して最適次数Ｍが決定できるように変更しなさい。もちろん，その最適モデルにおけるスペクトルや時系列予測の状況は，元のプログラムと同様に図示されるようにすること。
来週の時間に提出せよ
作成したプログラムとスペクトルや時系列予測の図を印刷して，来週の授業時間までに提出してください。

補足解説

Yule-Walker法
Yule-Walker法によるARモデルのあてはめは，MATLABでは，単に
a=aryule(x,M)
とするだけで済んでしまう。しかし，京大生なら，どういう計算を行っているのか理解しておこう。演習の前に少し解説する予定です。まず，Yule-Walker法は，基本的に以下ような計算を行っている。
r = xcorr(x,'biased');　% autocorrelation　R(-N+1) ～ R(-1),R(0) ～ R(N-1) r(1:length(x)-1) = [];　% R(0) ～ R(N-1) ay2 = levinson(r,M)
つまり，自己共分散関数（'biased'：データの無いところを0と見なして計算する自己共分散関数の推定値で，準正定値性をもつ）を求め，行列の形に書くと以下のようになる
Yule-Walker方程式をその係数行列のToeplitz性をいかしたLevinsonのアルゴリズムによって解くのである。
同じことは，次のような計算（最小二乗型一般逆行列）によっても実現できる。
Cfull = convmtx(x,M) ;　　　　% convolution matrix of x G = Cfull; d = [x([2:N]);zeros(M,1)];　　% add M zeros to (N+1)th through (N+M)th row a = G\d;　　　　　　　　　　　% generalized inverse : inv(G'*G)*(G'*d) ay1 = [1 -a']
つまり，われわれは，つぎの観測方程式がおおよそ満足されるようにAR係数を定めたいのである。

観測データの無いところは0として，この方程式を最小二乗法的に解くのが上に示したコードであり，それがすなわちYule-Walker方程式を解くことと同じになる。
Levinson-Durbinのアルゴリズム
Yule-Walker方程式を効率よく解く方法であるLevinson-Durbinのアルゴリズムを書き下せば，以下のようになる。講義で解説したことをMATLABで書くと，こんなコードになるのですが，理解できますか？　　Levinson-Durbinのアルゴリズムの詳しい解説はこちら
%　　　　　　Levinson-Durbin algorithm % var = r(1);　　　% initial　var: variance of prediction error ; R(0) ref = [1]; 　　　%　　　　　ref: reflection coefficients (-AR coefficients) cor = [r(1)];　　　　%　　　cor: autocorrelation vector 　　　; R(0) for k = 1:M　　　　　% iteration 　ref = [ref;0];　　　　　　　　　　% add a zero element to ref vector 　cor = [cor;r(k+1)];　　　　　　　 % add a element R(k) to cor vector 　am = (ref'*flipud(cor)) / var;　　% PARCOR coefficient 　ref = ref - am*flipud(ref);　　　 % new ref 　var = var*(1-am^2);　　　　　　　 % new var end ay3 = ref' %

今日の例題 「 ＡＲモデルの同定 」

今週の課題

補足解説

今日の例題「ＡＲモデルの同定」